10. Градиентные методы решения задач оптимизации.
 Градиент
– вектор, направленный в сторону наискорейшего возрастания функции. Вектор, противоположный градиенту, называется
отрицательным градиентом. Градиент
целевой функции grad f(x) – если целевая функция непрерывна и
дифференцируема, то существует ее градиент, определяемый как вектор – столбец,
составленный из частных производных целевой функции по всем факторам:
Градиент
– вектор, направленный в сторону наискорейшего возрастания функции. Вектор, противоположный градиенту, называется
отрицательным градиентом. Градиент
целевой функции grad f(x) – если целевая функция непрерывна и
дифференцируема, то существует ее градиент, определяемый как вектор – столбец,
составленный из частных производных целевой функции по всем факторам:
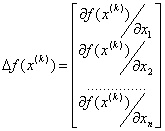
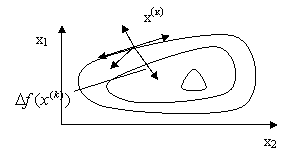
Градиент всегда
направлен перпендикулярно к линии уровня в данной точке. Длина вектора
градиента: ![]() . Суть всех градиентных методов заключается в
использовании вектора градиента для определения направления движения к
оптимуму. Согласно необходимому условию существования экстремума функции в
точке экстремума градиент функции обращается в ноль. Это
свойство часто используется для проверки условия окончания поиска в градиентных
методах, т.е.
. Суть всех градиентных методов заключается в
использовании вектора градиента для определения направления движения к
оптимуму. Согласно необходимому условию существования экстремума функции в
точке экстремума градиент функции обращается в ноль. Это
свойство часто используется для проверки условия окончания поиска в градиентных
методах, т.е. ![]() . Общий алгоритм всех градиентных методов заключается в
построении из некоторой начальной точки х(0)
последовательности приближений: x(k+1) = x(k)
- λ(k) S(k), где S(k) – единичный вектор в
направлении градиента f(x) в точке x(k), λ(k) – величина шага в направлении
градиента.
. Общий алгоритм всех градиентных методов заключается в
построении из некоторой начальной точки х(0)
последовательности приближений: x(k+1) = x(k)
- λ(k) S(k), где S(k) – единичный вектор в
направлении градиента f(x) в точке x(k), λ(k) – величина шага в направлении
градиента.
Градиентные методы с дроблением шага.
Методы с постоянным шагом.
Величина шага
αk
выбирается: ![]() , где 0 < ε < 1 - произвольно выбранная постоянная величина. При
минимизации функции выбираем α
> 0. На k-й итерации проверяем выполнение неравенства при αk
= α. Если оно
выполнено, полагаем αk = α и переходим к следующей итерации. Если нет, то шаг αk
дробим до тех пор, пока оно не выполнится.
, где 0 < ε < 1 - произвольно выбранная постоянная величина. При
минимизации функции выбираем α
> 0. На k-й итерации проверяем выполнение неравенства при αk
= α. Если оно
выполнено, полагаем αk = α и переходим к следующей итерации. Если нет, то шаг αk
дробим до тех пор, пока оно не выполнится.
Метод наискорейшего спуска или крутого восхождения Бокса - Уилсона.
Метод
наискорейшего спуска – это процесс, на каждой итерации которого шаг αk выбирается из условия
минимума функции f(x) в направлении движения,
т.е. ![]() .
.
 В этом методе направление движения из точки xk
касается линии уровня в точке xk+1. Последовательность точек x0, x1, … , xk, зигзагообразно приближается к точке
минимума х*, причем звенья этого зигзага
ортогональны между собой. Шаг α выбирается из условия минимизации по α функции
В этом методе направление движения из точки xk
касается линии уровня в точке xk+1. Последовательность точек x0, x1, … , xk, зигзагообразно приближается к точке
минимума х*, причем звенья этого зигзага
ортогональны между собой. Шаг α выбирается из условия минимизации по α функции ![]() ,
поэтому
,
поэтому ![]() .Т.о., направления спуска на двух
последовательных итерациях взаимно ортогональны.
.Т.о., направления спуска на двух
последовательных итерациях взаимно ортогональны.