1. Модель парной линейной регрессии. Метод наименьших квадратов для оценки параметров уравнения регрессии и проверка его адекватности.

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитическая связь между ними описывается уравнениями:

Прямой - , Гиперболы , Параболы

Модель линейной регрессии (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными.

Определить тип уравнения можно, исследуя зависимость графически.

Сущность МНК заключается в нахождении параметров модели (а₀, а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии: . Проводят дифференцирование S по коэффицентам и приравнивают уравнения к 0.

Из системы уравнений, получаем: 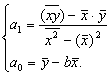 Здесь

Параметр а₁ называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на единицу.

После того как получено уравнение множественной регрессии, необходимо измерить тесноту связи между результативным признаком и факторными признаками. Для измерения степени совокупного влияния отобранных факторов на результативный признак рассчитывают совокупный коэффициент детерминации R² и совокупный коэффициент множественной корреляции R - общие показатели тесноты связи многих признаков.

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке):

.

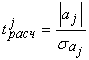Коэффициент регрессии считается статистически значимым, если  превышает t_табл  - табличное (теоретическое) значение t-критерия Стьюдента.

Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации .

Значение средней ошибки аппроксимации, определяемой по формуле

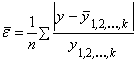 не должно превышать 12 - 15 %.

Расчетное значение F-критерия определяется по формуле и сравнивается с табличным:

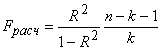 , где - коэффициент множественной детерминации.

Если F_расч  >F_табл, связь признается существенной.